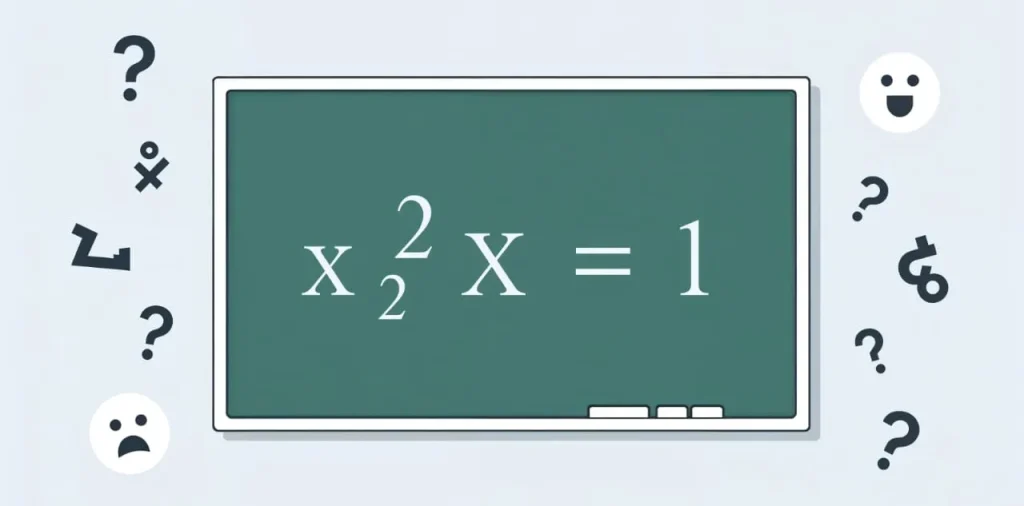Math puzzles can seem simple at first, but sometimes they hide tricky twists. One viral post captured this perfectly by presenting an equation that looks easy—but leaves almost everyone scratching their heads.
What’s the Equation?
The brain-teaser goes like this:
x² − x = x(x − 1)
At first glance, it seems like basic algebra. In fact, the two sides are identical once you expand the right-hand side. But that’s where things get sneaky.
The Sneaky Mistake
When people solve it, they often divide both sides by x(x−1) to simplify. That gives a weird result:
1 = 1
Or in some reasoning, it leads to 0 = 1, which, of course, makes no sense. This false conclusion usually comes from dividing by something that might be zero—a step we can’t always do safely.
Why Dividing by Zero is a Problem?
In math, division by zero is undefined because it breaks the rules of arithmetic. When you divide by a number, you’re essentially asking, “How many times does this number fit into the original value?” But zero can never be multiplied by anything to give a non-zero result—so division by zero doesn’t make logical sense.
That’s why, even if algebra seems to allow it, dividing by something that could be zero can lead to contradictions and false results.
Finding the Real Answer
The key is to go back to the original equation and test values that make x(x−1) = 0:
- If x = 0, we get 0 − 0 = 0(−1) → 0 = 0. It works.
- If x = 1, we get 1 − 1 = 1(0) → 0 = 0. This works, too.
So the real solutions are x = 0 and x = 1—but these were lost because someone wisely (or mistakenly) cancelled out terms without checking.
Graphical View of the Equation
If you graph both sides of the equation, you’ll see they produce the same parabola. This confirms that both expressions are algebraically equal, not just symbolically. But even graphs can mislead if you don’t check domain restrictions—especially where terms may become undefined.
Common Situations Where This Happens
This mistake isn’t unique to this puzzle. Similar traps appear in equations like:
(x² – 9)/(x – 3) = x + 3
At first glance, you might cancel and say the expression equals x + 3, but at x = 3, you’re dividing by zero! Always check if you’re eliminating a value that’s part of the solution.
The Lesson Here
This puzzle is a classic reminder: never divide by something before checking if it’s zero. It’s a simple rule, but easy to miss if you’re rushing.
That little mistake often brings great surprise: a puzzle that looked easy, but taught a powerful math lesson.
Real-Life Takeaway
Whether you’re coding, calculating finances, or solving formulas, a tiny overlooked rule—like dividing by zero—can lead to serious errors. Critical thinking in small steps helps prevent big mistakes.
If you’d like more brain-teasers like this, let me know — I love sharing clever puzzles!
Credit: Inspired by:
- Wordle Magazine article on the hardest math equation that stumps everyone.
- The Guardian Magazine article on How to Multiply by a Fraction?
Conclusion
At first glance, the equation x² − x = x(x − 1) may look straightforward, but it reveals how easily even seasoned problem-solvers can be tripped up by a small but critical error—dividing by zero. This deceptively simple puzzle serves as a powerful reminder that in mathematics, careful attention to rules and details is essential. It’s not just about solving equations—it’s about how we solve them. Missteps like ignoring domain restrictions or dividing by expressions that could be zero are common traps that lead to false conclusions. In the real world, whether in coding, engineering, or finance, these little miscalculations can have big consequences. So next time you’re working through a problem, take a moment to double-check your steps. Sometimes the hardest math puzzles aren’t the ones with complex numbers—but the ones that hide lessons in plain sight.