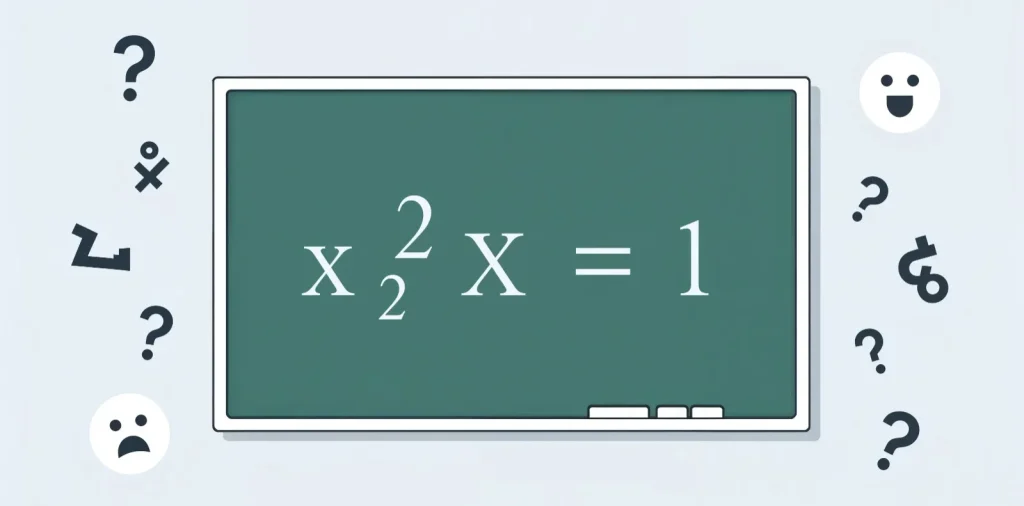Mathematics is full of challenging problems, but some stand out due to their complexity, mystery, and the number of great minds they’ve confounded for years. In the world of unsolved and complex mathematical problems, a few equations are so difficult that they’ve become legends. These equations don’t just baffle students—they stump mathematicians, computer scientists, and researchers around the world.
Also Read: Military Drones: Revolutionizing Modern Warfare Worldwide
What Makes a Math Equation “Hard”?
Before we reveal the toughest equation, let’s understand what makes a math problem hard. Several factors contribute to the difficulty of a mathematical problem:
- Abstract concepts – Problems that require understanding of abstract mathematical theories.
- Lengthy or complex solutions – Equations that need multiple steps, complex proofs, or advanced techniques.
- Lack of known solutions – Some equations remain unsolved even after decades or centuries.
- Computational challenges – Problems that cannot be solved using brute-force methods due to the sheer size or complexity.
When an equation combines most or all of these traits, it earns a reputation as being among the hardest.
What’s the Equation?
The brain-teaser goes like this:
x² − x = x(x − 1)
At first glance, it seems like basic algebra. In fact, the two sides are identical once you expand the right-hand side. But that’s where things get sneaky.
The Sneaky Mistake
When people solve it, they often divide both sides by x(x−1) to simplify. That gives a weird result:
1 = 1
Or in some reasoning, it leads to 0 = 1, which, of course, makes no sense. This false conclusion usually comes from dividing by something that might be zero—a step we can’t always do safely.
Finding the Real Answer
The key is to go back to the original equation and test values that make x(x−1) = 0:
- If x = 0, we get 0 − 0 = 0(−1) → 0 = 0. It works.
- If x = 1, we get 1 − 1 = 1(0) → 0 = 0. This works, too.
So the real solutions are x = 0 and x = 1—but these were lost because someone wisely (or mistakenly) cancelled out terms without checking.
Why Is the Riemann Hypothesis So Hard?
The Riemann Hypothesis is difficult for several reasons:
- It involves complex numbers
Most people are familiar with real numbers, but the Riemann Hypothesis operates in the complex number domain. This alone makes the equation hard to visualize and solve. - It connects to prime numbers
The zeta function is deeply tied to the distribution of prime numbers. A proof would unlock deep insights into how primes are spaced—something that has fascinated mathematicians for centuries. - No known general solution
Despite being tested on billions of zeros, and no counterexample ever being found, nobody has been able to prove the hypothesis for all cases. - It underpins modern cryptography
Solving it could potentially alter the foundation of modern encryption, which relies on the difficulty of factoring large prime numbers.
The Lesson Here
This puzzle is a classic reminder: never divide by something before checking if it’s zero. It’s a simple rule, but easy to miss if you’re rushing.
That little mistake often brings great surprise: a puzzle that looked easy, but taught a powerful math lesson.
If you’d like more brain-teasers like this, let me know — I love sharing clever puzzles!
Credit: Inspired by the Wordle Magazine article on the hardest math equation that stumps everyone.